Este post trata sobre un ejemplo tomado del Libro: Digital Signal Processing Using MATLAB and Wavelets, de Michael Weeks, Capítulo 3.
Básicamente, existen principalmente tres tipos de filtros: pasabajas que dejan pasar solamente bajas frecuencias; pasaaltas que dejan pasar altas frecuencias y pasabanda que permiten el paso de todo el espectro, no es menester de este ejemplo el explicar en teoría que es un filtro (eso tomaría demasiado) ni tratar el diseño de los mismos (eso tomaría aún más).
El nombre FIR viene de la manera en que el filtro afecta una señal. Una función impulso es una entrada bastante interesante, donde la señal es 0 siempre, excepto en un lugar donde tiene valor de 1 (una unidad). Se llama también delta Dirac en tiempo continuo y delta Kronecker en discreto (shhh!). La respuesta de un filtro FIR a esta entrada es de duración finita, y por lo consiguiente se le da este nombre.
Suponiendo que la Figura 1 tiene una entrada x[n] = [1,0]. La salida sería [0.5,0.5], y cero después de eso. Se pueden obtener estas salidas aplicándolas en orden a la estructura del filtro. En el tiempo 0, x[0] aparece en la entrada, y cualquier cosa antes de esto es cero, que es lo que el elemento delay producirá como salida. En el siguiente intervalo de tiempo x[0] será la salida del delay mientras que x[1] será la entrada actual.
y[0] = 0.5x[0] + 0.5x[-1]
y[1] = 0.5x[1] + 0.5x[0]
esto se generaliza como:
y[n] = 0.5x[n] + 0.5x[n-1]
La Figura 2 muestra la forma general de un filtro FIR, para K+1 coeficientes (son K+1, porque se empieza en 0 y se cuenta hasta K). El número de coeficientes también es llamado taps. Por convención el número de taps es igual al número de coeficientes. Así que un filtro con coeficientes {b0, b1, …, bK} tiene K+1 taps, debido a que tiene K+1 coeficientes. De todas maneras se dice que el orden es K. En otras palabras el orden del filtro y los taps expresan lo mismo pero con diferencia de 1.
Con la estructura de la Figura 2 es posible determinar la salida. También es posible determinar la ecuación de la salida, la cual es:
y[n] = b[0]x[n-0] + b[1]x[n-1] + b[2]x[n-2] + … + b[K]x[n-K]
Nótese que para cualquier índice que se usa para b[.] es usado en x[n-.]. Esto significa que podemos representar todo lo que se encuentra al lado derecho de la ecuación como una sumatoria:
¡Hey!, eso parece como una convolución, ¿no es así?
Un filtro pasabajas, puede llamarse también filtro promediador, mientras que un pasaaltas, puede ser llamado filtro diferenciador, debido a que estos términos describen el funcionamiento de los filtros.
Por ejemplo, un filtro FIR con dos coeficientes de 0.5 y 0.5, se observa que la salida es:
y[n] = 0.5x[n] + 0.5x[n-1], o equivalentemente y[n]=(x[n]+x[n-1])/2
dicha salida, encuentra el promedio entre la entrada actual y la anterior. Si se observa la respuesta a la frecuencia de dicho filtro, se observa que las partes de bajas frecuencias (cambian lentamente) aparecen en la salida, mientras que el filtro decrementa las partes de altas frecuencias (cambian rápidamente).
Para el filtro de diferencias, se pueden tener coeficientes de {0.5 , –0.5} donde:
y[n]=(x[n]-x[n-1])/2
Esto da el cambio entre las dos muestras, escalado por 1/2 para ser consistente con el filtro de promedios. Como es de esperarse, la respuesta a la frecuencia de dicho filtro, debe atenuar las partes de cambios lentos en la señal, y enfatizar la parte que cambia rápidamente, concluyendo que es un filtro pasaaltas.


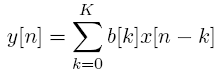
Muy bueno el post ¡Recomendado ¡
ResponderEliminarExcelente artículo!! Felicitaciones por la simpleza y la capacidad de síntesis
ResponderEliminar