¿Cómo demonios se supone que debo interpretar esto? Cuantización escalar uniforme de una imagen en MATLAB

Una parte fundamental del procesamiento digital de imágenes, es la representación de una imagen. De manera muy general, si vemos una imagen como parte de un sistema de adquisición de datos, el sensor es el que se encarga de capturar el brillo de la luz y convertirla a valores que puedan ser usados digitalmente, es nuestro convertidor análogo a digital. De acuerdo a lo que establece Sonka, Hlavac y Boyle en Image Processing, Analysis, and Machine Vision (Ed. Thompson, 2008, USA), la transición entre los valores continuos de la función de la  imagen (brillo) y sus equivalentes en el mundo digital se le llama cuantización, y el número de niveles de cuantización debe ser lo suficientemente grande como para permitir que el ser humano perciba los detalles finos del sombreado en la imagen. 

En este ejemplo vamos a trabajar con una imagen PGM, que al leerla en MATLAB nos regresa una matriz de tamaño NxM. Cada elemento representa un pixel en la imagen, con valores que van de 0 a 255, es decir 256 valores diferentes (8bits). A esta imagen también le podemos aplicar una cuantización ya que con menos bits es posible representar la imagen, con pérdidas debido a que son menos niveles de grises disponibles para mostrar la imagen.

1. %Lee imagene PGM
2. imagen = double(imread('peppers.pgm'));
3. %Crea variables temporales
4. imgQuantized = zeros(512,512);
5. imgQuantizedToDisplay = zeros(512,512);
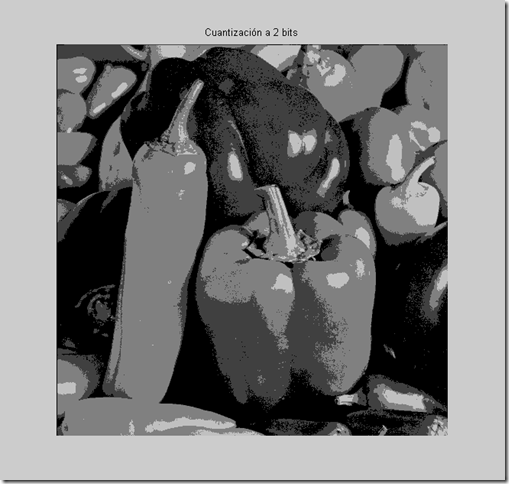
6. n = 2; %Define bits para cuantización
7. figure();
8. imgQuantized = floor(imagen/(256/(2^n)-1)); %Cuantizar
9. imgQuantizedToDisplay = ((imgQuantized)*(256/2^n));
10. imshow(uint8(imgQuantizedToDisplay));
11. title(['Cuantización a ', num2str(n) ,' bits']);
12. n = 4; %Define bits para cuantización
13. figure();
14. imgQuantized = floor(imagen/(256/(2^n)-1)); %Cuantizar
15. imgQuantizedToDisplay = ((imgQuantized)*(256/2^n));
16. imshow(uint8(imgQuantizedToDisplay));
17. title(['Cuantización a ', num2str(n) ,' bits']);
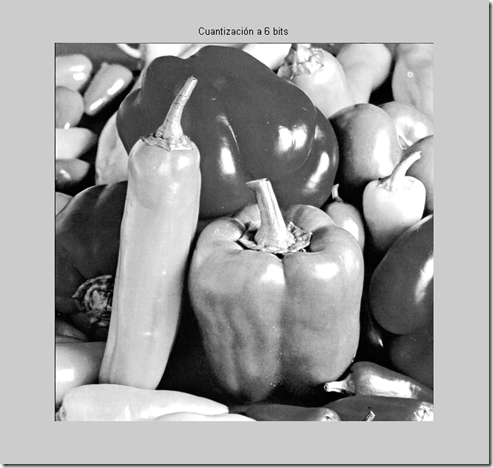
18. n = 6; %Define bits para cuantización
19. figure();
20. imgQuantized = floor(imagen/(256/(2^n)-1)); %Cuantizar
21. imgQuantizedToDisplay = ((imgQuantized)*(256/2^n));
22. imshow(uint8(imgQuantizedToDisplay));
23. title(['Cuantización a ', num2str(n) ,' bits']);

 

Con n=2 bits podemos representar 2^n=2^2=4 niveles distintos de grises. Así mismo, con n=4 bits podemos representar 2^n=2^4= 16 niveles y con n=6 bits se representan 2^n=2^6=64 niveles en escala de grises.