Implementación de un cuantizador “midtread” en MATLAB 7.0

La cuantización es el paso necesario para convertir una señal analógica a una digital, cuando se muestrea una señal se convierte del mundo analógico al mundo digital, y es necesario expresarlo en 0s y 1s, dícese bits. Aunque no necesariamente es el proceso de una señal analógica per se, puede ser también, por ejemplo, una imagen que necesita ser representada con una cantidad menor de bits, y por lo consiguiente comprimirla, con pérdidas claro está.

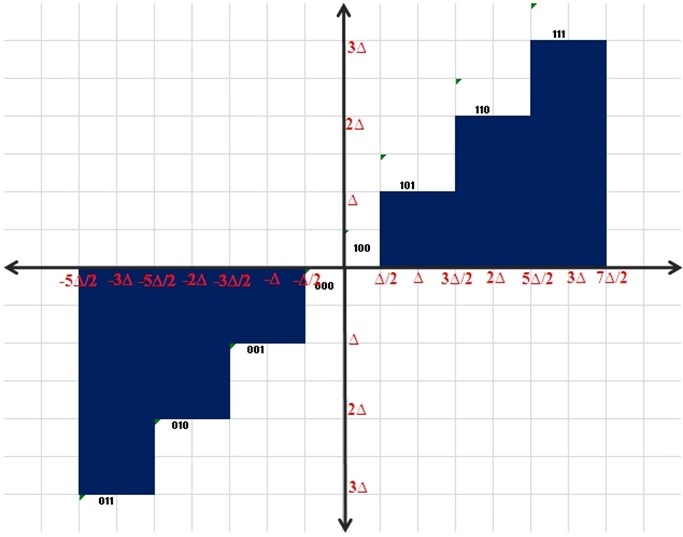
Existen variados tipos de cuantización. El tipo de cuantizador se elige dependiendo de la aplicación en que vaya a ser implementado, esto, de acuerdo a las características de la señal. En este caso se hará un pequeño ejemplo con un cuantizador midtread la grafica siguiente muestra el comportamiento de un cuantizador midtread de 3bits.

Figura 1. Características de un cuantizador midtread de 3 bits

El principal uso de este cuantizador es cuando tenemos una señal simétrica en el espectro positivo y negativo, por ejemplo una señal de audio, aunque también se puede aplicar en una imagen, como se muestra en el párrafo siguiente.

En la Figura 1 el eje equis (x) representa la señal a cuantizar y el eje ye (y) es la información ya cuantizada, delta () son los incrementos en los que se va a dividir la señal y esto depende del número de bits que sea el cuantizador, de lo anterior se puede desprender la siguiente tabla:

Código binario	Nivel de Cuantización (y)	Rango de la señal de entrada (x)
011	-3∆	–3.5∆ <= x < –2.5∆
010	-2∆	–2.5∆ <= x < –1.5∆
001	-1∆	–1.5∆ <= x < –0.5∆
000	0	–0.5∆ <= x < 0
100	0	0 <= x < 0.5∆
101	1∆	0.5∆ <= x < 1.5∆
110	2∆	1.5∆ <= x < 2.5∆
111	3∆	2.5∆ <= x < 3.5∆

La variable delta (∆) puede ser calculada de la siguiente manera

Ora si, vamos a ver el siguiente ejemplo, tenemos la señal de entrada x(n) = 254 254 252 254 255 253 y el rango válido de datos es de 250 a 255, que bien puede ser parte de una imagen ;) .

El primer paso es calcular delta.

Sustituyendo ∆ en la tabla anterior tenemos:

Código binario	Nivel de Cuantización (y)	Rango de la señal de entrada (x)
011	-3(0.71428) = -2.14284	–2.5 <= x < –1.7857
010	-2(0.71428) = -1.42856	–1.7857 <= x < –1.07142
001	-1(0.71428) = 0.71428	–1.07142 <= x < –0.35714
000	0	–0.35714 <= x < 0
100	0	0 <= x < 0.35714
101	1(0.71428) = 0.71428	0.35714<= x < 1.07142
110	2(0.71428) = 1.42856	1.07142 <= x < 1.7857
111	3(0.71428) = 2.14284	1.7857 <= x < 2.5

Para poder tener los datos de forma como se muestra en la Figura 1, es necesario definir cual es la media de nuestro rango, que en este caso es:

Si restamos a la señal de entrada la media obtenida en el paso anterior tenemos que:

x(n) – µ = 1.5 1.5 -0.5 1.5 2.5 0.5

ahora el siguiente paso es cuantizar cada valor utilizando la tablita arriba descrita…

x(0) = 1.5, cae entre 1.07142 y 1.7857 a lo cual corresponde un valor de cuantización de 1.42856 o sea 110 binario.

x(1) = 1.5, cae entre 1.07142 y 1.7857 a lo cual corresponde un valor de cuantización de 1.42856 o sea 110 binario.

x(2) = –0.5, cae entre –0.35714 y –1.07142 a lo cual corresponde un valor de cuantización de –1.42856 o sea 010 binario.

x(3) = 1.5, cae entre 1.07142 y 1.7857 a lo cual corresponde un valor de cuantización de 1.42856 o sea 110 binario.

x(4) = 2.5, cae entre 1.7857 y 2.5 a lo cual corresponde un valor de cuantización de 2.14284 o sea 111 binario.

x(5) = 0.5 cae entre 0.35714 y 1.07142 a lo cual corresponde un valor de cuantización de 1.42856 o sea 010 binario.

A continuación se presenta el código en MATLAB 7.0 para llevar a cabo esta cuantización:

x = [254 254 252 254 255 253];

bits = 3;
rango_superior = 255;
rango_inferior = 250;

delta = (rango_superior - rango_inferior)/((2^bits)-1)

mu = ((rango_superior - rango_inferior)/2) + rango_inferior

x_centrada = x - mu

x_cuantizada = floor(x_centrada/delta+0.5) * delta

y los resultados son:

delta =

    0.7143

mu =

  252.5000

x_centrada =

    1.5000    1.5000   -0.5000    1.5000    2.5000    0.5000

x_cuantizada =

    1.4286    1.4286   -0.7143    1.4286    2.8571    0.7143

DPCM (Differential Pulse Code Modulation), Método diferencial para compresión de señales, Parte I, puro rollo

La teoría del siguiente choro mareador y las figuras pirateadas fueron tomad@s de:
Data Compression: The Complete Reference. David Salomon. Fourth Edition. Springer. 2007. Section 4.26: DPCM
Digital Signal Processing: Fundamentals and Applications. Li Tan. Academic Press. 2008. Section 11.3: Examples of Differential Pulse Code Modulation, and Adaptive DPCM G.721

La compresión por DPCM es parte de la familia de métodos compresión por codificación diferencial. La idea general es usar valores pasados recuperados como base para predecir el dato actual de entrada. Esto se basa en el hecho, por ejemplo, que los pixeles en una imagen o muestras adyacentes en el audio digitalizado se encuentran correlacionadas. Los valores correlacionados son generalmente similares, así que sus diferencias son pequeñas, esto resultando en una compresión.
A continuación se muestra el esquema simple de compresión diferencial para poder entender el principio del DPCM.



                           Codificador                                 Decodificador

Figura 1. CoDec Diferencial

La imagen anterior muestra un ejemplo de un codificador diferencial, se observa como el dato actual se almacena en una unidad de almacenamiento, llámese “Delay” (o retardo pues si no les gusta agringarse), para ser usado para codificar el siguiente dato, o sea, . Claro, la explicación anterior esta sumamente simplificada, en este ejemplo se muestra el uso de un cuantizador, eso significa que se tiene una compresión con perdidas o “lossy” y esto significa que nuestro dato codificado es realmente el cual ya contiene un error de cuantización. Esto significa que la codificación por diferencias (o diferencial, como ustedes gusten y manden) nos mete en un nuevo problema: La acumulación de errores.

Entonces hay que tomar ventaja de lo que se menciona anteriormente, los datos que se van a comprimir están correlacionados. Esto significa que en general un dato depende de varios de sus vecinos, no solamente del anterior. Una mejor predicción puede ser lograda usando N de los datos previos para codificar el valor actual , entonces tendremos una función , para predecir el dato actual .

Ora si, en seguida pueden observar (jeje, como visita al museo) el diagrama del DPCM. (oooooohhhh!)


                          Codificador                                   Decodificador

Figura 2. DPCM

Oquey, oquey, haber encuentren la(s) diferencia(s) entre la Figura 1 y la Figura 2. ¿Está fácil? ¿que no? …

…

…

Pues si, cambiamos “Delay” por “Pred.” y se acabo el asunto.

Si.

Como se explicaba antes, el predictor viene siendo la funcioncica esta:

En donde tenemos que es una función que nos afecta un conjunto de N pixeles y en base a esto obtenemos una mejor predicción de nuestro valor actual, es decir tratamos de minimizar el error introducido por la cuantificación.

Esta es la primera parte de dos, en esta ocasión fue el rollo previo a un ejemplo peque para poder explicar la DPCM.